![]()
Cuando se habla en fotometría de magnitudes y unidades de media se definen una serie de términos y leyes que describen el comportamiento de la luz y sirven como herramientas de cálculo. Pero no hemos de olvidar que las hipótesis utilizadas para definirlos son muy restrictivas (fuente puntual, distribución del flujo esférica y homogénea, etc.). Aunque esto no invalida los resultados y conclusiones obtenidas, nos obliga a buscar nuevas herramientas de trabajo, que describan mejor la realidad, como son las tablas, gráficos o programas informáticos. De todos los inconvenientes planteados, el más grave se encuentra en la forma de la distribución del flujo luminoso que depende de las características de las lámparas y luminarias empleadas.
 |
 |
 |
A menudo no le daremos mucha importancia a este tema, como pasa en la iluminación de interiores, pero será fundamental si queremos optimizar la instalación o en temas como la iluminación de calles, decorativa, de industrias o de instalaciones deportivas.
A continuación veremos los gráficos más habituales en luminotecnia:
En estos gráficos la intensidad luminosa
se representa mediante un sistema de tres coordenadas (I,C,![]() ). La primera de ellas I representa el valor numérico de la
intensidad luminosa en candelas e indica la longitud del vector mientras las otras señalan la
dirección. El ángulo C nos dice en qué plano vertical estamos y
). La primera de ellas I representa el valor numérico de la
intensidad luminosa en candelas e indica la longitud del vector mientras las otras señalan la
dirección. El ángulo C nos dice en qué plano vertical estamos y ![]() mide la inclinación respecto al eje
vertical de la luminaria. En este último, 0º señala la vertical hacia abajo, 90º
la horizontal y 180º la vertical hacia arriba. Los valores de C utilizados en las gráficas
no se suelen indicar salvo para el alumbrado público. En este caso, los ángulos entre
0º y 180º quedan en el lado de la calzada y los comprendidos entre 180º y 360º en la
acera; 90º y 270º son perpendiculares al bordillo y caen respectivamente en la calzada y en la
acera.
mide la inclinación respecto al eje
vertical de la luminaria. En este último, 0º señala la vertical hacia abajo, 90º
la horizontal y 180º la vertical hacia arriba. Los valores de C utilizados en las gráficas
no se suelen indicar salvo para el alumbrado público. En este caso, los ángulos entre
0º y 180º quedan en el lado de la calzada y los comprendidos entre 180º y 360º en la
acera; 90º y 270º son perpendiculares al bordillo y caen respectivamente en la calzada y en la
acera.

Con un sistema de tres coordenadas es fácil pensar que más que una representación plana tendríamos una tridimensional. De hecho, esto es así y si representamos en el espacio todos los vectores de la intensidad luminosa en sus respectivas direcciones y uniéramos después sus extremos, obtendríamos un cuerpo llamado sólido fotométrico. Pero como trabajar en tres dimensiones es muy incómodo, se corta el sólido con planos verticales para diferentes valores de C (suelen ser uno, dos, tres o más dependiendo de las simetrías de la figura) y se reduce a la representación plana de las curvas más características.
En la curva de distribución luminosa, los radios representan el ángulo ![]() ylascircunferencias concéntricas
el valor de la intensidad en candelas. De todos los planos verticales posibles identificados por el
ángulo C, solo se suelen representar los planos verticales correspondientes a los planos de
simetría y los transversales a estos (C = 0º y C = 90º) y aquel en que la lámpara
tiene su máximo de intensidad. Para evitar tener que hacer un gráfico para cada
lámpara cuando solo varía la potencia de esta, los gráficos se normalizan para una
lámpara de referencia de 1000 lm. Para conocer los valores reales de las intensidades
bastará con multiplicar el flujo luminoso real de la lámpara por la lectura en el
gráfico y dividirlo por 1000 lm.
ylascircunferencias concéntricas
el valor de la intensidad en candelas. De todos los planos verticales posibles identificados por el
ángulo C, solo se suelen representar los planos verticales correspondientes a los planos de
simetría y los transversales a estos (C = 0º y C = 90º) y aquel en que la lámpara
tiene su máximo de intensidad. Para evitar tener que hacer un gráfico para cada
lámpara cuando solo varía la potencia de esta, los gráficos se normalizan para una
lámpara de referencia de 1000 lm. Para conocer los valores reales de las intensidades
bastará con multiplicar el flujo luminoso real de la lámpara por la lectura en el
gráfico y dividirlo por 1000 lm.
 |
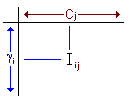
También es posible encontrar estos datos en unas tablas llamadas matriz
de intensidades luminosas donde para cada pareja de valoresde C y ![]() obtenemos un valor de I normalizado para una lámpara de
flujo de 1000 lm.
obtenemos un valor de I normalizado para una lámpara de
flujo de 1000 lm.
A pesar de que las curvas de distribución luminosa son herramientas muy útiles y prácticas, presentan el gran inconveniente de que sólo nos dan información de lo que ocurre en unos pocos planos meridionales (para algunos valores de C) y no sabemos a ciencia cierta qué pasa en el resto. Para evitar estos inconvenientes y conjugar una representación plana con información sobre la intensidad en cualquier dirección se definen las curvas isocandela.
En los diagramas isocandelas se representan en un plano, mediante curvas de nivel, los puntos de igual valor de la intensidad luminosa. Cada punto indica una dirección del espacio definida por dos coordenadas angulares. Según cómo se escojan estos ángulos, distinguiremos dos casos:
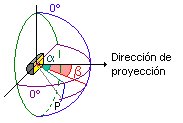
En los proyectores se utiliza un sistema de coordenadas rectangulares con ángulos en lugar de las típicas x e y. Para situar una dirección se utilizaun sistema de meridianos y paralelos similar al que se usa con la Tierra. El paralelo 0º se hace coincidir con el plano horizontal que contiene la dirección del haz de luzy el meridiano 0º con el plano perpendicular a este. Cualquier dirección, queda pues, definida por sus dos coordenadas angulares. Conocidas estas, se sitúan los puntos sobre el gráfico y se unen aquellos con igual valor de intensidad luminosa formando las líneas isocandelas.
 |
 |
En las luminarias para alumbrado público, para definir una
dirección, se utilizan los ángulos C y ![]() usados en los diagramas polares. Se supone la luminaria situada
dentro de una esfera y sobre ella se dibujan las líneas isocandelas. Los puntos de las curvas se
obtienen por intersección de los vectores de intensidad luminosa con la superficie de esta. Para
la representación plana de la superficie se recurre a la proyección azimutal de Lambert.
usados en los diagramas polares. Se supone la luminaria situada
dentro de una esfera y sobre ella se dibujan las líneas isocandelas. Los puntos de las curvas se
obtienen por intersección de los vectores de intensidad luminosa con la superficie de esta. Para
la representación plana de la superficie se recurre a la proyección azimutal de Lambert.

En estos gráficos, los meridianos representan el ángulo C, los paralelos ![]() y las intensidades, líneas rojas, se reflejan en
tanto por ciento de la intensidad máxima. Como en este tipo de proyecciones las superficies son
proporcionales a las originales, el flujo luminoso se calcula como el producto del área en el
diagrama (en estereorradianes) por la intensidad luminosa en este área.
y las intensidades, líneas rojas, se reflejan en
tanto por ciento de la intensidad máxima. Como en este tipo de proyecciones las superficies son
proporcionales a las originales, el flujo luminoso se calcula como el producto del área en el
diagrama (en estereorradianes) por la intensidad luminosa en este área.
Además de intensidades y flujos, este diagrama informa sobre el alcance y la dispersión de la luminaria. El alcance da una idea de la distancia longitudinal máxima que alcanza el haz de luz en la calzada mientras que la dispersión se refiere a la distancia transversal.
Las curvas vistas en los apartados anteriores (diagramas polares e isocandelas) se obtienen a partir de características de la fuente luminosa, flujo o intensidad luminosa, y dan información sobre la forma y magnitud de la emisión luminosa de esta. Por contra, las curvas isolux hacen referencia a las iluminancias, flujo luminoso recibido por una superficie, datos que se obtienen experimentalmente o por calculo a partir de la matriz de intensidades usando la fórmula:
![]()
Estos gráficos son muy útiles porque dan información sobre la cantidad de luz recibida en cada punto de la superficie de trabajo y son utilizadas especialmente en el alumbrado público donde de un vistazo nos podemos hacer una idea de como iluminan las farolas la calle.
Lo más habitual es expresar las curvas isolux en valores absolutos definidas para una lámpara de 1000 lm y una altura de montaje de 1 m.

Los valores reales se obtienen a partir de las curvas usando la expresión:
![]()
También puede expresarse en valores relativos a la iluminancia máxima (100%) para cada altura de montaje. Los valores reales de la iluminancia se calculan entonces como:
Ereal = Ecurva · E máx
con
![]()
siendo a un parámetro suministrado con las gráficas.