1. Una superficie está iluminada por una fuente luminosa puntual de 80 cd de intensidad constante en todas direcciones situada a 2 m de altura. Calcular la iluminancia horizontal y vertical para los siguientes valores del ángulo alfa: 0, 30º, 45º, 60º, 75º y 80º.
Como vimos al hablar de magnitudes fotométricas, las componentes de la iluminancia, se pueden calcular empleando las fórmulas:
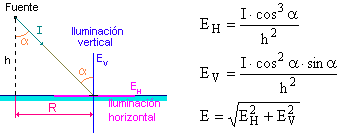
Y dado que conocemos todos los datos (h = 2 m, I = 80 cd y los diferentes valores de alfa) solo queda sustituir y calcular:
Como podemos ver, la mecánica de cálculo es siempre la misma. Así pues, los resultados finales son:
 |
R (m) | EH (lux) | EV (lux) | E (lux) |
|---|---|---|---|---|
| 0º | 0 | 20 | 0 | 20 |
| 30º | 1.15 | 12.99 | 7.5 | 15 |
| 45º | 2 | 7.07 | 7.07 | 10 |
| 60º | 3.46 | 2.5 | 4.33 | 5 |
| 75º | 7.45 | 0.35 | 1.29 | 1.34 |
| 80º | 11 | 0.10 | 0.59 | 0.60 |
Si representamos el diagrama isolux de la superficie podemos observar que las curvas son circunferencias, debido a que la intensidad es constante en todas direcciones, que la iluminancia disminuye a medida que los puntos se alejan del foco y que la máxima iluminancia se encuentra en la proyección de la fuente sobre la superficie (0º).
2. Una superficie circular de 3 m de radio está iluminada por una bombilla de 50 cd de intensidad constante en todas direcciones situada a 2 m de altura sobre el centro de la plataforma. Calcular la iluminación máxima y mínima sobre la superficie.
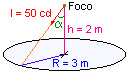En este caso nos piden la
iluminancia sobre la superficie, es decir, la iluminancia horizontal. Como la intensidad es constante en
todas direcciones y la altura también el valor de la iluminancia dependerá
únicamente de la distancia de los puntos al foco. En nuestro caso el punto más
próximo es la proyección de la bombilla sobre la superficie ( = 0º) y los más alejados son aquellos que están en los bordes
(R = 3 m).
Iluminancia máxima:
Iluminancia mínima (R = 3 m):
3. Tenemos un proyector situado en el techo de 0.04 m2 de superficie que ilumina con una intensidad de 100 cd en cualquier dirección una mesa de 0.5 m2 de superficie. La mesa se puede considerar una superficie especular de factor de reflexión de 0.8. Calcular la luminancia de la fuente y la luminancia de la mesa para el observador de la figura.
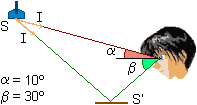
Luminancia de la fuente:
Luminancia de la mesa:
Como la mesa no es una superficie reflectante perfecta una parte de la intensidad luminosa que le llega es absorvida por esta. Esto quiere decir que en la fórmula de la luminancia el valor de I estará afectado por el factor de reflexión.
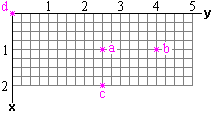
4. Tenemos una luminaria simétrica situada en el centro de una habitación de 5 x 2 m a 3 m de altura del suelo. Calcular la iluminancia sobre los puntos marcados en el dibujo a partir del diagrama polar de la luminaria. El flujo luminoso de la lámpara es de 500 lm.
 |
 |
En este caso la intensidad no es uniforme ni constante en cualquier dirección y por ello tenemos que trabajar con gráficos. Esto no supone ninguna complicación adicional respecto a lo visto anteriormente y la mecánica y las fórmulas empleadas siguen siendo las mismas. La única diferencia estriba en que los valores de la intensidad los tomaremos de un gráfico polar, que en este caso depende sólo del ángulo alfa debido a que la luminaria es simétrica.
Los pasos a seguir son:
) relativo del gráfico
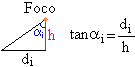
Iluminancia en a:
Iluminancia en b:
Iluminancia en c:
Iluminancia en d:
5. Un tramo de calle está iluminado por una farola de 10 m de altura y 10000 lm de flujo luminoso cuyo diagrama isolux se adjunta.
Calcular la iluminancia en los siguientes puntos de la calzada:
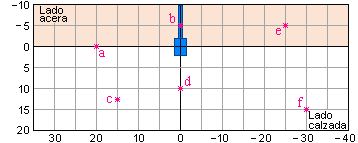
Resolver este problema es muy sencillo, pues sólo hay que trasladar los puntos de la calle al diagrama isolux dividiendo sus coordenadas por la altura de la luminaria, leer los valores del gráfico y calcular la iluminancia con la fórmula.
Iluminancia en c:
Las coordenadas absolutas de c son: x = 15 m e y =12.5 m
Ahora las dividimos por la altura (10 m) para convertirlas en valores relativos que situaremos sobre el gráfico:
xr = 1.5 ; yr = 1.25
A continuación leemos los valores relativos de la iluminancia del diagrama:
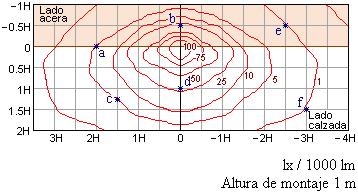
| Coordenadas relativas | Er (lx/1000 lm) |
|---|---|
| (1.5,1.25) | 5 lx |
Finalmente aplicamos la fómula y ya está.
Como se puede ver el proceso a seguir es siempre igual y los resultados finales son:
| Punto | Coordenadas absolutas |
Coordenadas relativas |
Er (lx/1000 lm) | E (lx) |
|---|---|---|---|---|
| a | (20,0) | (2,0) | 100 | 10 |
| b | (0,5) | (0,0.5) | 25 | 2.5 |
| c | (15,12.5) | (1.5,1.25) | 5 | 0.5 |
| d | (0,10) | (0,1) | 25 | 2.5 |
| e | (25,5) | (2.5,0.5) | 1 | 0.1 |
| f | (30,15) | (3,1.5) | 1 | 0.1 |
1. Tenemos una fuente luminosa puntual de 100 cd deintensidad constante en todas direcciones situada sobre una plataforma rectangular de 20x10 m como la de la figura. Calcular la iluminación máxima y mínima sobre la superficie y la iluminancia en los puntos(3, 10), (0, 15), (7, 20) y (10, 15).
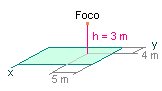
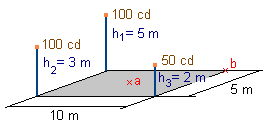
2. Para la disposición de luminarias de la figura, calcular la iluminancia en el centro de la placa (a) y en el punto b.
3. Para el tramo de calle de la figura, calcular la iluminancia en los puntos a, b, c, d, e y f. La farola mide 8 m de altura y la lámpara tiene un flujo de 15000 lm. Asimismo, se suministran los diagramas polares de las luminarias referenciadas a 1000 lm.
 |
 |
4. Para el tramo de calle de la figura calcular las iluminancias de los puntos a, b, c y d a partir dela matriz de intensidades luminosas de la luminaria.
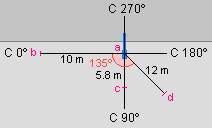
Otros datos: h = 10 m |
|
 |
 |
|
 |
|
Como la intensidad es constante en
todas direcciones y la altura también el valor de la iluminancia depende sólo de la
distancia de los puntos al foco. El punto más próximo es la proyección de la fuente
sobre la superficie (15,4) y el más alejado es (10,0).
= 15000 lm
