| Per començar | Elements d'entrada | Programació CircuitPython | Recursos CITCEA | |
| Elements no electrònics | Elements de sortida | Programació Arduino | ||
| Projectes | Elements de control | Dades pràctiques | Inici |
La Terra no és una esfera perfecta però podem suposar que ho és per a molts càlculs senzills. Els sistema de coordenades més habitual és el que es basa en la latitud i la longitud, que és el que fan servir els sistemes GPS. Amb la latitud i la longitud podem definir un punt qualsevol sobre l'esfera ideal, caldrà tenir en compte també l'altitud per tenir la posició exacta d'un punt qualsevol.
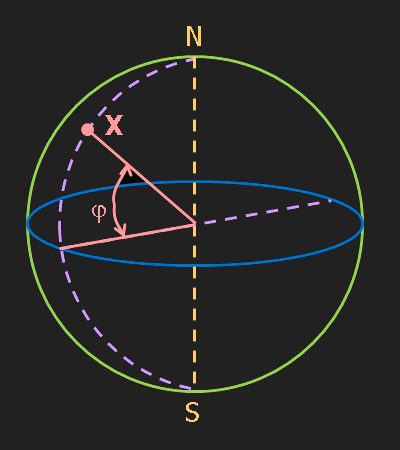
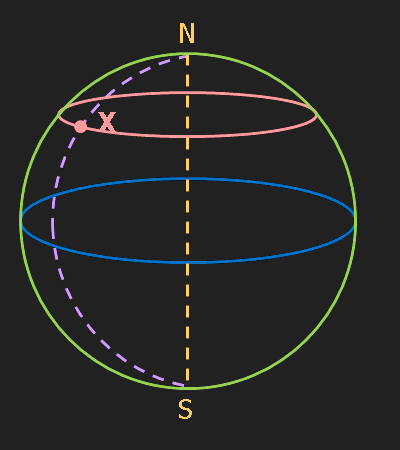
La latitud, representada per φ, és l'angle d'aquest punt respecte a l'equador. Un punt situat a l'equador tindrà una latitud de 0°, un situat al pol nord la tindrà de 90° i un del pol sud de -90°. Els valors, doncs, poden anar de -90° a 90°. A vegades s'indica el sentit amb una N o una S en lloc de fer servir el signe. Tots els punts situats en el mateix paral·lel tenen la mateixa latitud.


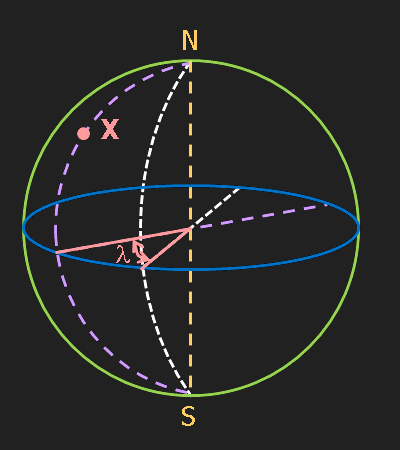
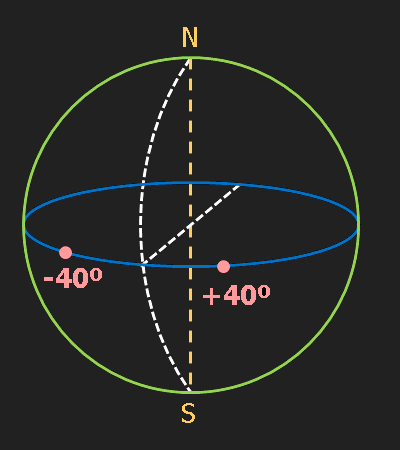
La longitud, representada per λ, és l'angle que correspon al meridià que passa pel punt. El meridià de Greenwich té una longitud de 0°. Els punts situats a l'est del meridià de Greenwich tenen longitud positiva i els situats a l'oest la tenen negativa. Els valors poden anar de -180° a 180°. A vegades, en lloc del signe, es fan servir les lletres E i O per indicar els dos sentits.
Per calcular distàncies que no siguin molt grans podem suposar que la Terra és esfèrica i prescindir de les diferències d'alçada; llavors la fórmula del haversine ens dóna una aproximació força bona entre dos punts dels que sabem la longitud i la latitud.
Per calcular la distància entre dos punts (φ1, λ1) i (φ2, λ2) aplicarem la fórmula del haversine:
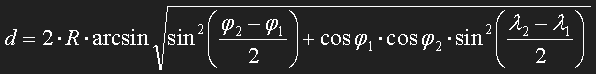
on R és el radi de la Terra, que val 6371 km.
Cal tenir en compte que les funcions trigonomètriques necessiten els angles en radians.

Aquesta obra d'Oriol Boix està llicenciada sota una llicència no importada Reconeixement-NoComercial-SenseObraDerivada 3.0.